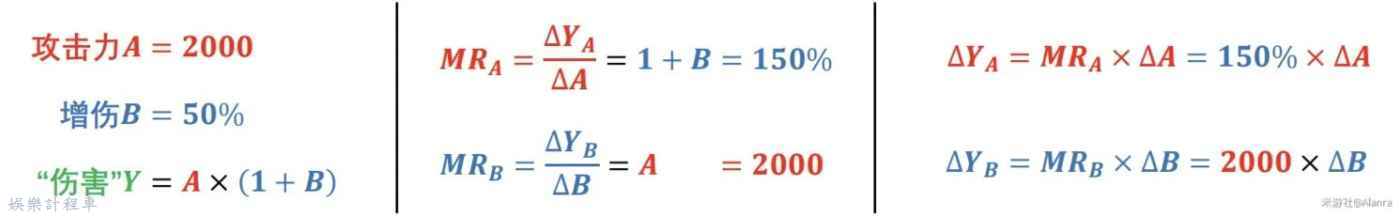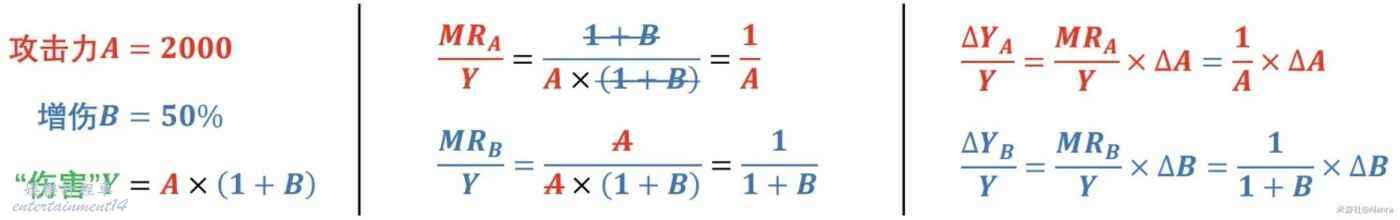作者:Alanra
來源:米遊社論壇
省流版結論
1.邊際收益:屬性變動1單位時,傷害變動了多少?
2.邊際收益率:屬性變動1單位時,傷害變動了百分之多少?
3.稀釋:邊際收益率遞減,隨著屬性的增加,每增加1單位帶來的「傷害變動百分比」不斷下降。
4.反稀釋:邊際收益率遞增,隨著屬性的增加,每增加1單位帶來的「傷害變動百分比」不斷上升。
5.除了「減防」和「雙爆的部分區間」是“反稀釋”以外,其他屬性均表現為“稀釋”。
6.如果「你不確定各個屬性要變動多少」,「稀釋理論」幾乎是唯一的通用方法。
6.如果「你很確定各個屬性要變動多少」,「比較收益率」是最精確簡單的方法。
引言
在第一次聽到「稀釋」、「反稀釋」或是「邊際收益」等概念時,不知道你有沒有感到一頭霧水。
「稀釋」的例子
同樣增加100攻擊,
在1000攻擊的時候,提升是10%;
在2000攻擊的時候,提升只有5%,
從10%降到5%,這就是「稀釋」。
這個例子簡單易懂,如果你能理解這個“收益率”的變化(10%→5%),那你就理解了「稀釋」的本質,其實就是「收益率下降」,“100攻擊帶來的收益”被“原本的攻擊”稀釋了。
「反稀釋」的例子
同樣增加10%減防,
在0%減防的時候,提升是5.3%;
在50%減防的時候,提升是7.1%,
從5.3%升到7.1%,這就是「反稀釋」。
類似的,「反稀釋」的本質,其實就是「收益率上升」。但想必有很多人會感到疑惑,這個5.3%和7.1%是咋來的?我們可以說,“10%減防帶來的收益”被“原本的減防”反稀釋了?
還有一些問題,
1.以上只是兩個例子,換個條件結論會變麼?
2.什麼導致了「稀釋」和「反稀釋」的不同?
3.「稀釋」怎麼來的,稀釋理論很重要麼?
4.如果攻擊稀釋比雙爆嚴重,一定首選雙爆?
本文將分析「稀釋」的由來與含義,逐步解答以上問題,並列出各個常見屬性的稀釋特點。
這所有的一切都源於傷害計算公式。
絕大多數的傷害計算帖都是根據這個公式進行分析,簡單來說,就是“改變某個屬性,看一下對傷害的影響”。那要如何衡量“對傷害的影響”,我們將從這裡開始。
邊際收益:傷害的導數
什麼是導數?為什麼需要導數?
邊際收益(Marginal Revenue, MR),是微觀經濟學中的概念,可以理解為收益的導數。
引入到遊戲裡,自然你也可以稱傷害的導數為邊際傷害(Marginal Damage, MD),但這裡,沿用邊際收益這一名詞。
邊際收益描述了,當屬性變動1單位時,傷害變動了多少?
例如,在攻擊2000、增傷50%的面板下,
我們可以看到,
攻擊邊際收益MR_A,只與增傷B有關;
增傷邊際收益MR_B,只與攻擊A有關。
對於它們各自而言,只要其他屬性不變,邊際收益就不會改變,不存在“邊際收益遞減”。
假設,現在要在60攻擊和5%增傷裡選一個,只需要計算「邊際收益MR×變動值」就行了。
在攻擊2000、增傷50%的面板下,
攻擊A加60,傷害增加150%×60=90。
增傷B加5%,傷害增加2000×5%=100。
因此,應該選5%增傷。但如果是100攻擊,傷害就增加150了,那就應該選攻擊。
從邊際收益出發,我們能夠得到一個較為簡單的量化和比較方法。
但這個方法有一個缺點,明明我想研究攻擊,卻要先知道增傷的數值,這有點麻煩。
由於乘法的特性,邊際收益(求導結果)不可避免地帶上來自其他乘區的變數。這使得各個變數交織在一起,要得到某個變數的邊際收益,必須先知道其他變數的值,無法獨立研究單個變數。
有沒有什麼辦法可以避免變數的耦合呢?有,邊際收益率。
邊際收益率與稀釋
邊際收益:x變動1單位時,y變動了多少,即△x與△y的關係。
邊際收益率:x變動1單位時,y變動的百分比是多少,即△x與△y/y的關係。
因此,邊際收益率=邊際收益÷y,即一階導數與原函數的比值。
還是剛剛的例子,但與邊際收益稍有不同。
「攻擊的邊際收益率」,只與「攻擊」有關,且隨著攻擊A的增大而減小;增傷亦然。
這種「邊際收益率遞減」的現象,就是所謂的「稀釋」。
那所謂的反稀釋,其實就是“邊際收益率遞增”。
「稀釋」不是「收益的下降」,事實上,每1點攻擊帶來的傷害提升都是一樣的。
「稀釋」是「收益率的下降」,隨著攻擊不斷堆疊,同樣1點攻擊帶來的傷害提升率在不斷下降,攻擊收益被稀釋了。
假設,還是在60攻擊和5%增傷裡選一個,此時要計算「邊際收益率×變動值」就行了。
在攻擊2000、增傷50%的面板下,
攻擊A加60,傷害增加60/2000=3%。
增傷B加5%,傷害增加5%/(1+50%)=3.33%。
因此,仍然選5%增傷。同樣,如果是100攻擊,傷害就增加100/2000=5%,那就應該選攻擊。
「稀釋」:誰稀釋了誰?
「稀釋」,指對現有溶液加入更多溶劑而使其濃度減小的過程。因此,稀釋這個詞的本意是“往糖水里加水”。
「濃縮」,指使溶劑蒸發而提高溶液的濃度,是與稀釋相對的概念。但耐人尋味的是,遊戲裡,大家不用這個詞,而是用「反稀釋」。
把「邊際收益率遞減」的現象稱為「稀釋」,這個習慣可能已然根深蒂固。
事實上,當我第一次聽到「稀釋」時,我並沒有一個清晰直觀的認識,相反,我感到非常疑惑。
什麼叫“攻擊稀釋”?糖和水分別是什麼?
如果攻擊是糖,難道往糖水里加糖,糖水會稀釋麼?
如果攻擊是水,那不加水不就更濃了麼,我應該減少攻擊?
原來,攻擊既是糖也是水,攻擊的增量是糖,攻擊的存量是水,攻擊的收益被攻擊自己稀釋了。
個人而言,我並不是很喜歡「稀釋」這個詞。
「稀釋」並沒有很自然地描述“邊際收益率遞減”的現象,無法讓新讀者快速get到含義。
但不可否認的是,「稀釋」足夠通俗,它在一定程度上是合理的,並承擔了代指的功能。
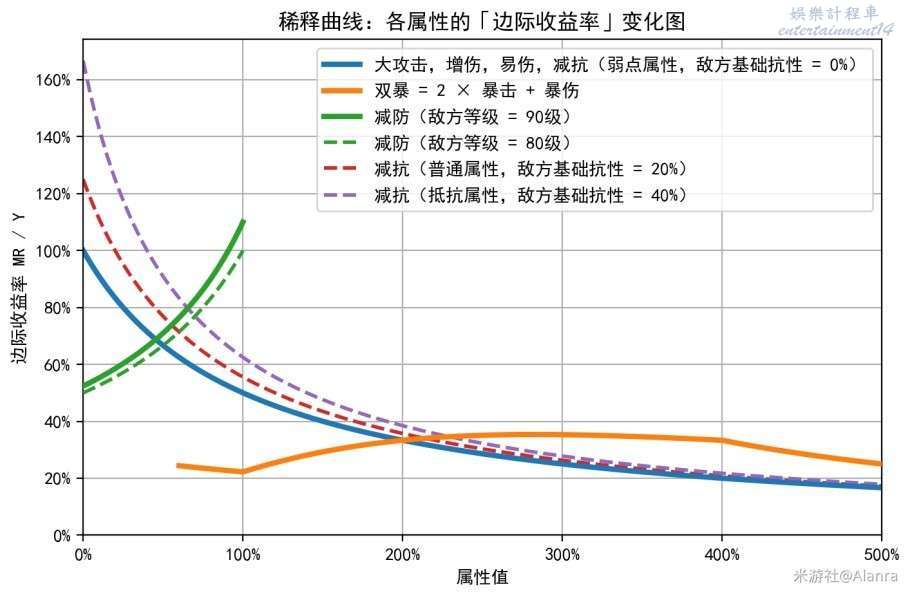
各屬性的「稀釋」現象
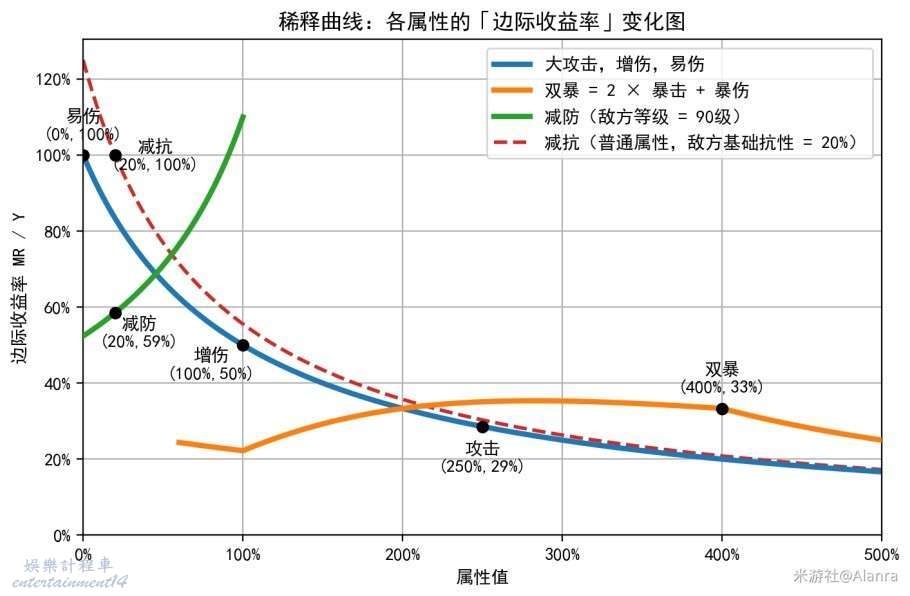
正如上文所述,「稀釋」現象,其實就是研究各屬性的邊際收益率。由於與該屬性無關的乘區是一個常數,因此在求邊際收益率的時候,分子分母相消,只需要聚焦於該屬性影響的乘區即可。下文將分析各個屬性的邊際收益率。
攻擊:稀釋
增傷:稀釋
雙爆:稀釋-反稀釋共存
減防:反稀釋
減抗:稀釋
易傷:稀釋
整理圖如下,可以看到,除了「減防」和「雙爆的部分區間」是“反向稀釋”以外,其他屬性均表現為“稀釋”。
「稀釋理論」的價值
理論價值>實用價值
「稀釋」似乎無處不在,然而,在看攻略計算帖的時候,你可能會發現在正文計算裡,幾乎看不到「稀釋」二字,也沒有關於「稀釋程度」的任何計算。why?
「稀釋理論」到底有什麼用?這裡有一個實例。
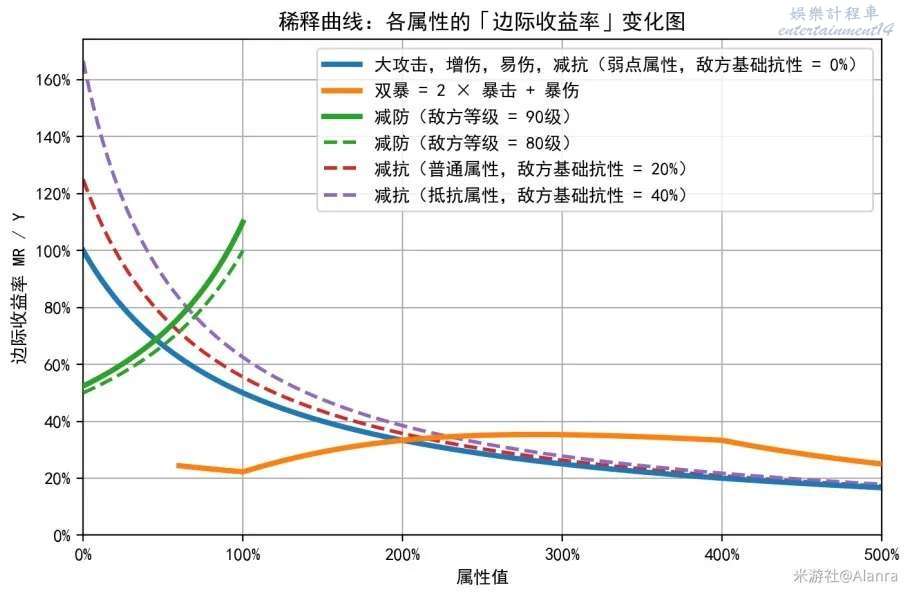
假設,人物面板如下:250%大攻擊,100%增傷,400分雙暴,20%減防,20%減抗,0%易傷。
把對應的點標在圖上,如下圖:
這意味著,如果1%易傷、1%攻擊、1%增傷等等裡挑一個,那應該首選易傷or減抗,
易傷=減抗>減防>增傷>雙暴>攻擊。
但問題是,如果不是相同的數值呢?5%攻擊和1%增傷裡挑呢?
因此,通常不能直接比較「稀釋程度」用於決策。
可以間接比較麼?可以,只要你能接受誤差
如果「你不確定各個屬性要變動多少」,「稀釋理論」幾乎是唯一的通用方法,提供一個宏觀泛用的結論。
如果「你很確定各個屬性要變動多少」,「比較收益率」是最精確簡單的方法,不必從「稀釋」裡分析。
實際應用中,確定的情況更多,這也是為什麼計算帖中很少用稀釋理論的原因。
評論和彈幕中,不確定的情況更多,因為篇幅有限,沒辦法詳細說明屬性數值。
價值理論:「稀釋」新說
看到這裡,也不知道我有沒有很好地解釋清楚「稀釋」,希望能幫大家明晰其中的含義。
前文提到,其實我不太喜歡「稀釋」這個詞,但好像很少有人提出新詞去代替它。畢竟要改變大眾的習慣,並不容易,但也值得一試。
仍沿用經濟學中的概念,
「價值」=「邊際收益率」
「貶值」=「邊際收益率遞減」=「稀釋」
「升值」=「邊際收益率遞增」=「反稀釋」
貶值嚴重的屬性,不代表沒有價值,只要給的足夠慷慨,依舊能與高價值屬性一較高下。