作者:zyl910
來源:文明6吧
一、原理
文明6裡有一些特殊的建築及奇觀,它們不僅對所屬城市有效,還能覆蓋一定範圍內的城市。
工業區(Industrial Zone)建築——
工廠(Factory):所在工業區6格半徑範圍內的所有城市 產能+3,大工程師點數+1
發電廠(Power Plant):所在工業區6格半徑範圍內的所有城市 產能+4,大工程師點數+1
娛樂區(Entertainment Complex)建築——
動物園(Zoo):所在娛樂中心6格半徑範圍內的所有城市滿意度(娛樂)+1
體育場(Stadium):所在娛樂中心6格半徑範圍內的所有城市滿意度(娛樂)+2
奇觀——
羅馬鬥獸場(Colosseum):所在格周圍6格半徑範圍內的所有城市文化+2、且滿意度(娛樂)+3
另外有個城邦還可能增加這個影響範圍——
多倫多(Toronto):宗主國的工業區與娛樂中心的區域效應範圍增加3格
故可通過仔細規劃城市佈局,構建一個共用區域,使範圍內的城市享受同時被多個工業區、娛樂區加成的效果。
數學苦手可以直接跳過後面的數學計算小節,直接看 “3.2 具體方案”(6格)、“4.2 具體方案”(9格)。
二、公式推導
2.1 背景知識
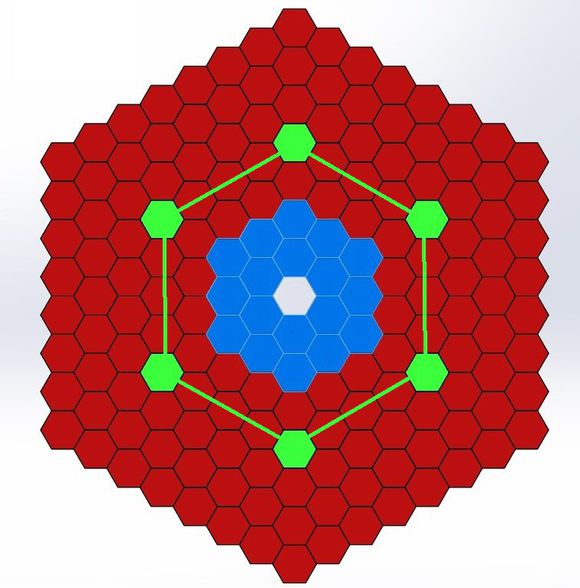
在六角形地圖裡,圓的概念如下:
這是一個半徑2的圓,在以下的說明裡記為R=2,可以看出圓內任何格到中心格的距離都≤2。
而城市的建設範圍是一個R=3的圓,如下圖所示:
R=3的圓最外層稱為R=3的環,環所包含的格數為6R,所有環上的格到中心格的距離都為3。
2.2 公式推導
設立代數——
L:工業區影響範圍常量(一般為6,多倫多城邦加成後為9)
A:所有城市中心包含在內的環半徑
B:把所有工業區包含在內的環半徑。A>=B
列不等式——
最大距離:A+B<=L
最小距離:A-B<=3
兩式相加——
(A+B) + (A-B) <= L+3
2*A <= L+3
A <= (L+3)/2
當已求出A時,可以求出B的最大環半徑:B=L-A
但要注意城市只能管理3格內,故最外圈城市可管理的距離 B’>=A-3 。
三、影響範圍為6時
3.1 計算
帶入L=6後得——
A <= (6+3)/2
A <= 4.5
A可取4。此時B = L-A = 6-4 = 2
即(幾何中心的)2環及以內是共用區。
最外圈城市可管理的距離——
B’>=A-3
B’>=4-3
B’>=1
即最外圈城市可管理的共用區為(幾何中心的)1環至2環的地塊。
3.2 具體方案
6格時的黃金6城(7城)方案已經被很多人討論透了,我這裡便不細說了。
共用區域規劃技巧初探
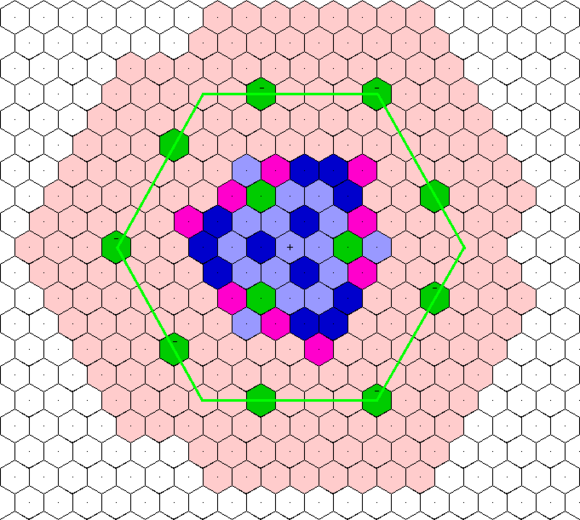
以黃金6城方案為例——
圖中綠色為城市中心,可以在R=4的環上任意轉動排列。
紅色為城市的建設範圍。
藍色為工業區和文化區應該建設的位置。只要建設在藍色區域,6城都可以享受。
所有的城市均受到6個工業區的加成。所加產能為 (3+4)*6 = 7*6=42。
所有的城市均受到6個娛樂區的加成。所加滿意度為 (1+2)*6 = 3*6=18。
注意這些加成不受其他因素影響。只要按本規劃建好城市,即使它是1人口小城,也能享受加成。
四、影響範圍為9時
4.1 計算
帶入L=9後得——
A <= (9+3)/2
A <= 6
A可取6。此時B = L-A = 9-6 =3
即(幾何中心的)3環及以內是共用區。
最外圈城市可管理的距離——
B’>=A-3
B’>=6-3
B’>=3
即最外圈城市可管理的共用區僅為(幾何中心的)3環地塊。
因A為6,即最外環城市中心的半徑為6。
6環共有36格。以平均每隔3格1個城市來看,那麼可以放 36/(3+1)=9個城市。
(幾何中心的)2環有12格,正好能放 12/(3+1)=3個城市。
即城市總數為 9+3 = 12。
4.2 具體方案
因內圈城市在(幾何中心的)2環,那麼 每個城市的1環會 在 幾何中心的3環 占3格,這幾格不適宜放工業區。
那麼3環還剩下 18-(3*3) = 9格格子。正好用來放外層9個城市的工業區。
內層的工業區看來得放在1環以內了。排除與城市中心相鄰的格子,正好剩下3格。
這樣就能使所有的城市均受到12個工業區的加成。所加產能為 (3+4)*12 = 7*12=84。
而對於娛樂區——
先說外圈。雖然理論上3環還剩下9格(18 – 9個工業區),正好可放下9個外圈城市的娛樂區。可只有6個城市的管理範圍夠,可將娛樂區能放在共用半徑內。而另外3個城市 因其管理範圍的3環 與 幾何中心的3環只有 1格相交,而那一格已用作工業區了,故會導致有3個娛樂區無法放入共用半徑。這4個娛樂區只能放在幾何中心的第4環了,可通過巧妙的對稱放置,使這3個娛樂區均能覆蓋10個城市中心(漏掉了2個外圈城市中心)。即外圈有6個城市,會均少1次娛樂區覆蓋。
內圈3個城市的的娛樂區可在3環內隨便放,覆蓋所有城市。
即——
內層3個城市與外層3個城市:被 12 個娛樂區覆蓋。所加滿意度為 (1+2)*12=3*12=36
外層6個城市:被11個娛樂區覆蓋。所加滿意度為 (1+2)*11=3*11=33
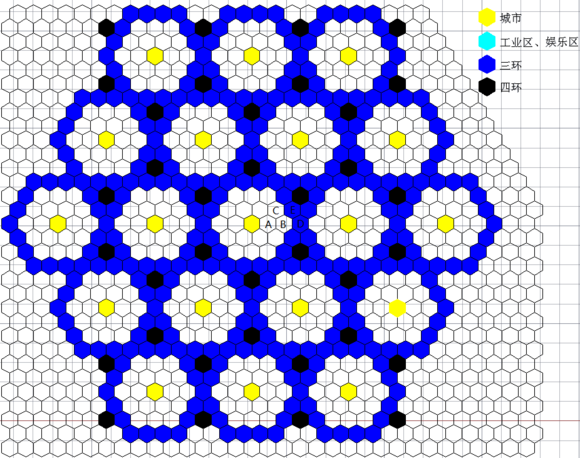
顏色說明——
綠色:城市中心(帶“-”的是少1個娛樂區覆蓋的)
深藍:工業區
亮藍:內層3個城市的娛樂區或自由格子
紫色:外層9個城市的娛樂區
淡紅色:非共用的城市建設範圍
最後還可以考慮在中心格子修一個“羅馬鬥獸場”奇觀。它也是影響6格的,12個城均能受到加成。
五、5格距平鋪時的工業區位置選擇
為了盡可能高效的占地,有時我們會採用5格距平鋪的形式來建城。只要陸地面積足夠,能鋪多少個城,便鋪多少。例如——
本節便是專門用來討論這種情況下的工業區位置選擇的。
5.1 標準方案
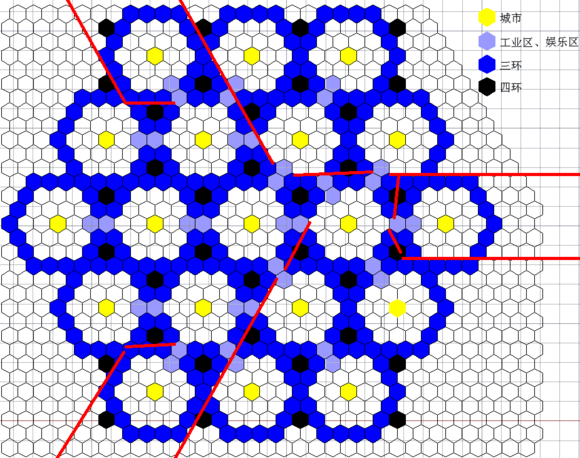
考慮到六邊形對稱,工業區的擺放位置實際上只有5種選擇(其他位置是這5個選擇的旋轉或鏡像)。即上圖的A、B、C、D、E。
計算了一下這5個位置範圍覆蓋情況——
A位置(1環直格):範圍為6時能覆蓋4城,為9時覆蓋7城。注意工業區有相鄰地格吸引力降低1的懲罰。
B位置(2環直格):範圍為6時能覆蓋4城,為9時覆蓋7城
C位置(2環偏格):範圍為6時能覆蓋3城,為9時覆蓋7城
D位置(3環直格):範圍為6時能覆蓋4城,為9時覆蓋10城
E位置(4環偏格):範圍為6時能覆蓋3城,為9時覆蓋9城
注——
直格:從城市中心出發,直走便能到達的格子。
偏格:從城市中心出發,需要拐彎才能到達的格子。
可見,最佳位置是D,不僅在平常情況下能覆蓋4城,且在有城邦將影響範圍為9時能覆蓋10城。
由於該城邦是可遇而不可求。故工業區位置的優先順序為 D、B、A、E、C。
娛樂區也是同理。擺好工業區後,按照該優先順序(D、B、A、E、C)放娛樂區。
5.2 加強中心的方案
在很多時候,我們希望加強中心城市的產能。
故可以將週邊城市分為6類,將工業區朝向中心。例如(方案不只一種)——
此時中心城市的工業區覆蓋情況——
範圍為6時:被7個城覆蓋(自己 + 圈1的6個城)。所加產能為 (3+4)*7 = 7*7=49。
範圍為9時:被19個城覆蓋(自己 + 圈1的6個城 + 圈2的12個城)。所加產能為 (3+4)*19 = 7*19=133。
該方案的優點是能使中心城市獲得很大的加成。
缺點是工業區的加成不是均勻的,除了中心城市外,其他城市只被少量工業區覆蓋。
5.3 推廣到其他格距或非一致距離
很多人鋪城時不是5格距離,而且很多時候由於地形限制,沒法全部保持5格距離。此時的工業區位置該怎麼擺呢?
從上述內容來看,工業區擺在直格(從城市中心出發,直走便能到達的格子)是最容易覆蓋更多城市的。
其次,選最遠(3環)的位置,會更容易覆蓋更多城市的。
故也可以按照 D、B、A、E、C 的優先順序放置工業區、娛樂區。
六、中心城市的理論最大加成
參考前幾節的經驗,現在可以估算中心城市的理論最大加成了。
為了獲得最大加成,故城市間距應該選3格。
以中心城市為中心,在外面的環上建城市——
第1圈城市位於中心城市的4環。共有 (6*4)/(1+3) = 24/4 = 6個城市。
第2圈城市位於中心城市的8環。共有 (6*8)/(1+3) = 48/4 = 12個城市。
第3圈城市位於中心城市的12環。共有 (6*12)/(1+3) = 72/4 = 18個城市。
……
第n圈城市位於中心城市的 4*n 環。共有 (6*(4*n))/(1+3) = 6*n 個城市。
6.1 影響範圍為6時
第2圈城市位於中心城市的8環,考慮到城市可管理3格範圍內的格子,那麼它們的工業區可放在5環上。
此時中心城市能受到 自身、第1圈城市、第2圈城市 的工業區加成。所加產能為 (3+4)*(1+6+12) = 7*19=133。
6.2 影響範圍為9時
第3圈城市位於中心城市的12環,考慮到城市可管理3格範圍內的格子,那麼它們的工業區可放在9環上。
此時中心城市能受到 自身、第1圈城市、第2圈城市、第3圈城市 的工業區加成。所加產能為 (3+4)*(1+6+12+18) = 7*37=259。